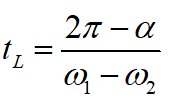Derivation of Hohmann orbit formulas
For a small body with mass m in an elliptic orbit about a much larger body with mass M, the total energy is
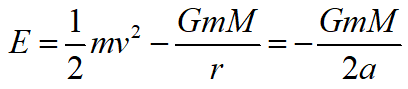
where r is the distance between the centers of the bodies and a is the semimajor-axis of the elliptic orbit.
Solving this equation for the velocity gives
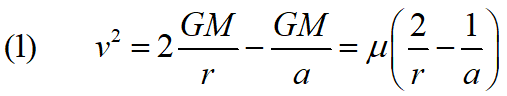
where μ = GM.
The speed in a circular orbit with radius r, where a = r, becomes
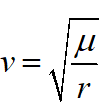
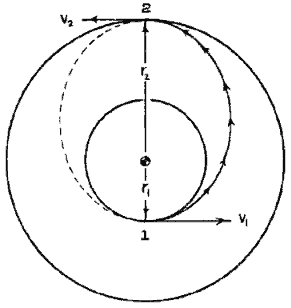
The drawing above shows that the semi-major axis is
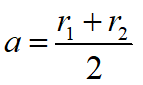
The necessary speed increase in the low circular orbit is the difference between the speed in the elliptic Hohmann orbit at r = r1 and the speed in the lower circular orbit:
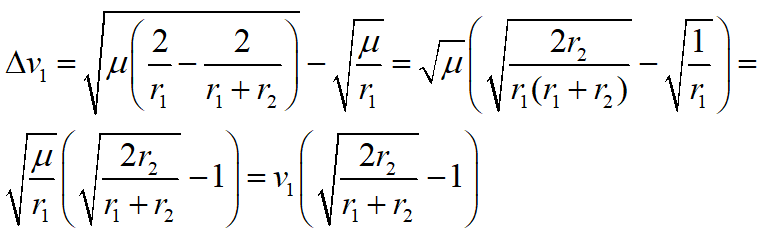
In a similar way we find the speed increase at r2 to achieve a circular orbit there:
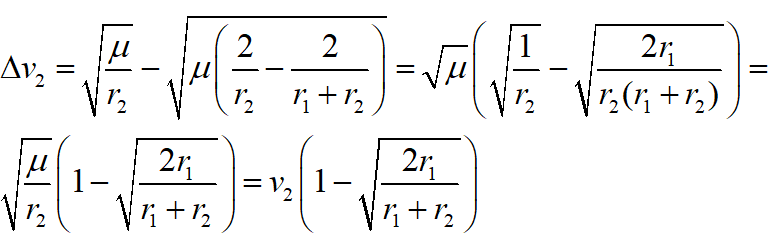
The time of transit in the Hohmann orbit is one half the period of the full elliptic orbit. Kepler's third law gives:
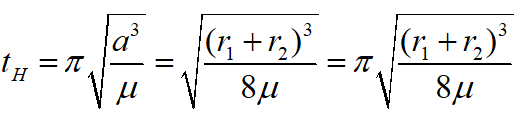
The following section is only relevant for the simulation "Hohmann transfer orbit to Mars".
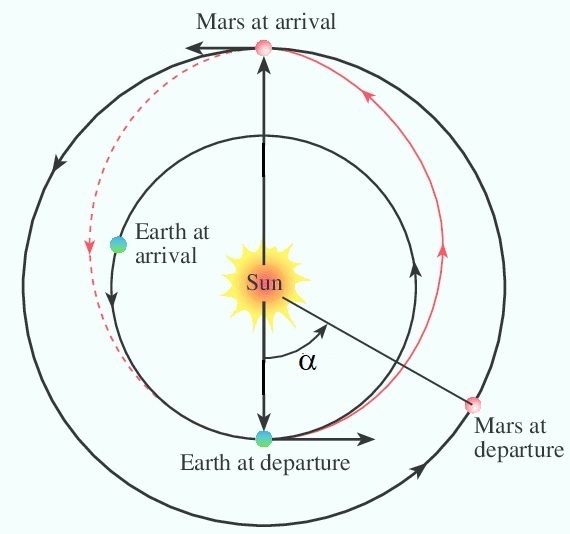
We now consider a Hohmann orbit where the spacecraft has to meet another body when it arrives at the outer orbit.
In the illustration below the outer body is Mars and the spacecraft leaves just outside the Earth.
The spacecraft has to leave the inner orbit when the angular displacement between the spacecraft and Mars has a certain value α, in this case 44o.
The period of Mars is
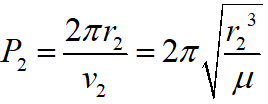
Then its angular velocity is
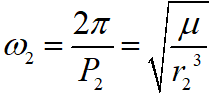
In the time tH Mars moves an angle ω2tH .
The spacecraft moves a larger angle π in the same time. So the angle between the spacecraft and Mars at the launch into the Hohmann orbit should be (in radians)
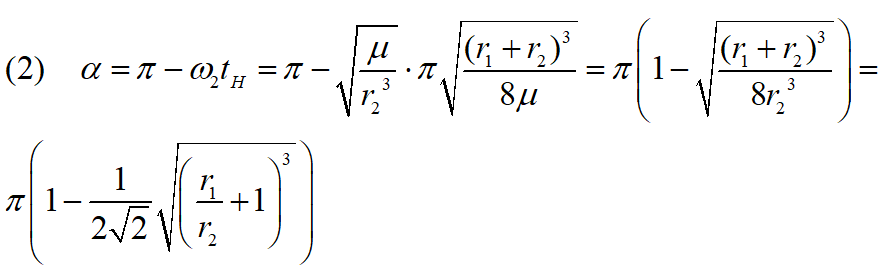
where Mars is ahead of the spacecraft.
In the simulation the angle between the spacecraft and Mars is zero. The angle at time t is
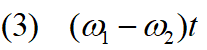
When does this angle become equal to the value in equation 2?
Simply setting the expression in (3) equal to α (from equation 2) will give the time when the spacecraft is the angle α ahead of Mars.
We have to wait until the angle between the two bodies is 2π - α to launch the spacecraft into the Hohmann orbit.
Therefore the time of launch is